Merkle Trees

Introduction

Let us assume that we are building a distributed data store. We store data in data blocks. There will be tens of thousands of data blocks, if not more. For availability reasons, we need to replicate the blocks across several nodes. While we try to keep the nodes in sync, it is possible that they go out of sync once in a while. How do we quickly identify such inconsistencies between replicas? Alternatively, consider a peer to peer network. A huge dataset is split into smaller chunks and nodes exchange chunks across themselves and reconstruct the dataset from the chunks that they receive from their peers. How do we ensure that the integrity of the original dataset? How do we ensure that some malicious node has not slipped in a modified chunk?

The answer to both these questions and many more are Merkle Trees. Merkle trees are hash trees that allows secure verification of contents of large data structures. Merkle trees are widely used across several applications, including hash based cryptography, Bitcoin/Ethereum and more. The well known Cassandra uses Merkle trees to identify data inconsitencies between replicas.

Implementation

At its heart, a Merkle tree is a tree of hashes. Leaf nodes contain hashes of data blocks. Parent nodes and root nodes store hashes of the children. The follwing picture explains this.

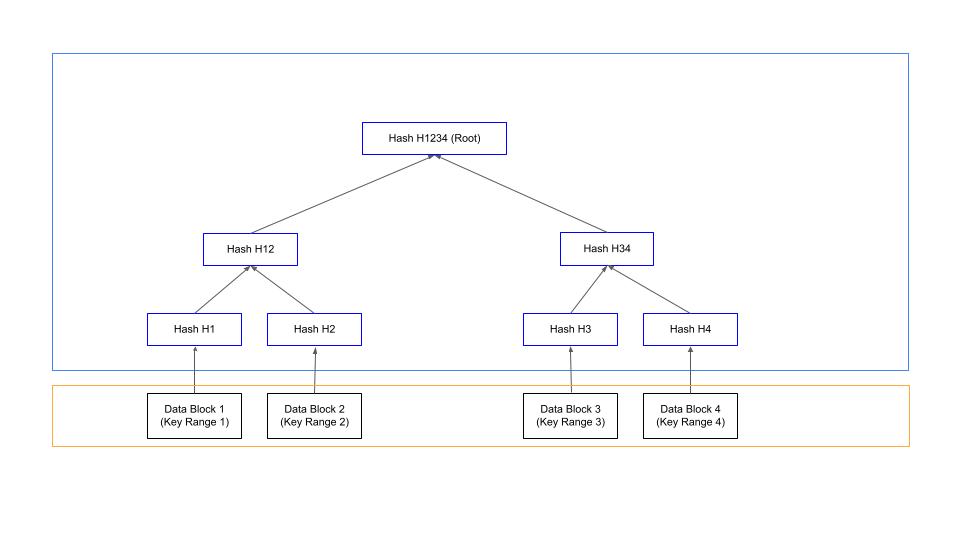
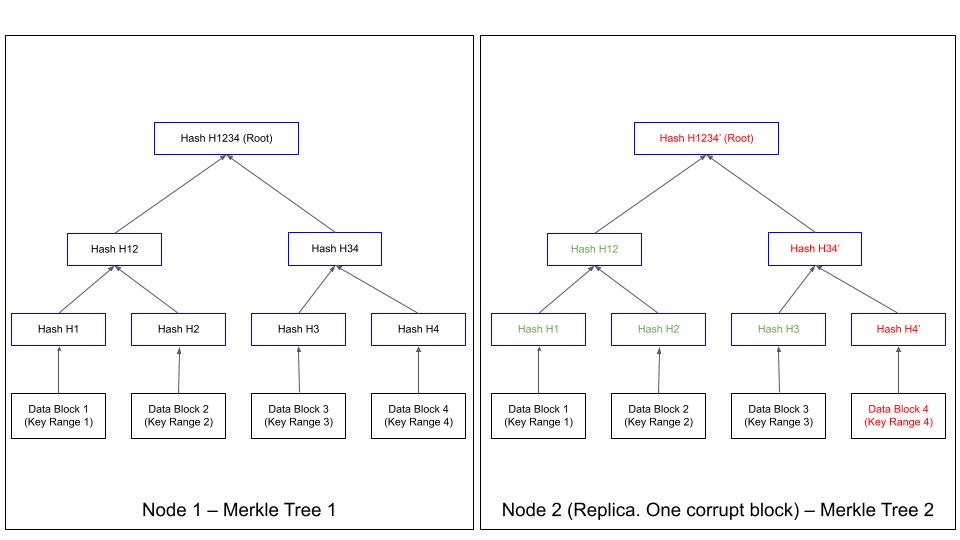
To compare if the contents of two replicas are in sync, we start comparing the root hashes. If they are identical, the replicas are in sync. If not, we compare the children of root to see where they differ. We keep going down the tree to the actual leaf node to identify the out-of-sync replicas. So, identification of a given data block typically involves log(n) verficiations of hashes, starting from the root. The following picture explains this. Here, the tree on the LHS is built on Node 1 and the tree on RHS is built on Node 2. Assuming that the DataBlock 4 is corrupt in Node 2, we start by comparing the Root Hash (H1234). Since this differs, we compare left node, Hash H12. This is the same on both the trees. So, the error is on the right tree. So, we compare H3, which again compares favourably. Hence the error is on H4 and since H4 is a leaf node, data block 4 should be the corrupt one.

The following is a simple code snippet for this.

    def compareTrees(self, leftTree: MerkleTree, rightTree: MerkleTree):
        if (leftTree is None and rightTree is None):
            return True

        if (leftTree is not None and rightTree is None):
            print("LT [%s], RT None" % leftTree.name)
            return False

        if (leftTree is None and rightTree is not None):
            print("RT [%s], LT None" % rightTree.name)
            return False
        
        if (leftTree.is_leaf() and not rightTree.is_leaf()):
            print("LT [%s] is a leaf, RT [%s] is not" % (leftTree.name, rightTree.name))
            return False
        elif (not leftTree.is_leaf() and rightTree.is_leaf()):
            print("LT [%s] is not a leaf, RT [%s] is" % (leftTree.name, rightTree.name))
            return False

        if (leftTree.get_digest() == rightTree.get_digest()):
            return True

        if (leftTree.is_leaf()): #Both are leaves
            if (leftTree.left_leaf.get_data_block() != rightTree.left_leaf.get_data_block()):
                print ("Discrepany found in left leaf. Left Tree %s, Right Tree %s" % (leftTree.name, rightTree.name))
                print(f"L-DB {leftTree.left_leaf.get_data_block()}, R_DB {rightTree.left_leaf.get_data_block()}")
            else:
                print ("Discrepany found in right leaf. Left DB %s, Right DB %s" % (leftTree.name, rightTree.name))
                print(f"L-DB {leftTree.right_leaf.get_data_block()}, R_DB {rightTree.right_leaf.get_data_block()}")

            return False       
        
        if (self.compareTrees(leftTree.get_left_tree(), rightTree.get_left_tree())):
            return self.compareTrees(leftTree.get_right_tree(), rightTree.get_right_tree())
        else:
            return False

The implementation of a Merkle Tree is fairly straight forward. Here is a Java implementaion. As outlined above, the “Leaf” class has an array of data blocks. The “MerkleTree” class has the digest, either of the data nodes or of the children.

Typically, most Merkle Tree implementations use a perfect binary tree where all leaves are at the same depth. Cassandra also uses a perfect binary tree. So, to support 2¹²⁷ tokens, a Merkle treee of depth 127 is required. This is expensive to build and the memory costs are high. Cassandra does an optimization where it restricts the depth to 15. It splits the keys into 32768 (2¹⁵) ranges and does an effecient comparison.

Summary

Whenever you next face a solution where you want to securely verify the integrity of distributed data, Merkle trees should list in the top of your options.

Redis Sorted Sets - Under the Hood

Character Encoding